生成式模型探索

2021-11-20 | 阅读：次

简述

工作中需要对jd职位描述生成一些具有总结性的话语，可以理解为自动文本摘要，因此尝试了如下模型，记录以下碰到的问题以及改进，话不多说，直接上干货吧~

先知

由于是工作探索阶段，因此没有很好的数据，具体方式如下：

通过训练NER提取关键词（这一步怎么来的就不再介绍），关键词组成的语句作为label；

Seq2seq+Attention

训练方式

jieba切词，词为单元训练
训练使用 teach forcing，预测使用 Beam search
encoder 和 decoder都使用 lstm

测试结果

停不下来寻因探究

ICML 2020的文章《Consistency of a Recurrent Language Model With Respect to Incomplete Decoding》比较系统地讨论了这个现象，并提出了一些对策。

seq2seq解码是一个”自回归“生成模型，$\color{blue}{p(y_t)|y<t,x}$，那么解码过程就是给定$\color{blue}{x}$来输出对应的$\color{blue}{y=(y_1,y_2,…,y_T)}$，解码算法大致分为$\color{red}{确定性解码和随机性解码}$，下面简单介绍以下这两种算法。

确定性解码

确定性解码就是输入固定的文本，解码出来的结果也是固定的，这类算法包括贪心搜索(Greedy Search)和束搜索(Beam Search)，其中贪心搜索就是束搜索的极端情况，Beam Search在前面blog中简单提过，其实就是每次选取top K概率最大的。
随机解码

随机性解码，就是输入固定输出却不固定，主要包括下面三种情况

1、原始采样随机解码，原始采样法是一种针对有向图模型的基础采样方法，指从模型所表示的联合分布中产生样本，又称祖先采样法。该方法所得出的结果即视为原始采样。具体的每步按概率随机采样一个token，比如第一步算$\color{blue}{p(y_1|y_0,x)}$，然后按照概率随机采样一个token，比如c；计算第二不，$\color{blue}{p(y_1|y_0,c,x)}$，再按随机概率采样一个token，比如a，依次下去，知道采样到停止。

2、top-k 随机解码：，出自文章$\color{yellow}{《Hierarchical Neural Story Generation》}$，就是再原生采样随机解码的基础上加了个截断，每一步只保留概率最高的$\color{blue}k$个token，然后重新归一化在采样，这么做是希望再“得分高”和“多样性”做了一个这种。$\color{bule}k=1$时，就是贪心搜索。

3、Nucleus随机解码：出自文章$\color{yellow}{《The Curious Case of Neural Text Degeneration》}$,跟top-k 随机解码类似，也是对采样空间做了截断，阶段方式是——固定$\color{blue}p\in(0,1)$，然后只保留概率最高的、概率和刚好超过$\color{blue}p$的若干token，所以也叫top-p 采样。

从seq2seq的模型设计和上面解码算法来看，理论上不能保证解码过程一定能停下来，只能靠模型学习，当模型学习不好的时候，就会出现根本停不下来的现象

停不下来怎么解决(这部分不知道咋回事公式识别不好，遂改成图片展示)

1、有界的隐向量，$\color{blue}{p(y_t|y<t,x)=softmax(Wh_t+b),h_t=f(y<t,x)}$是建模概率，计算个隐向量，然后全连接，softmax激活，如果对任意的$\color{blue}t,| |h_t| |$是有上界的，那么原始采样解码就能”停止“。说简单点就是只要你采样够多，就能停，实际应用价值就不大了。

2、1的方法是针对原始采样方法的，对top-k 随机解码和Nucleus随机解码就不一定成功了，因为不一定会出现再采样空间，要想使用只能手动把添加到采样空间。

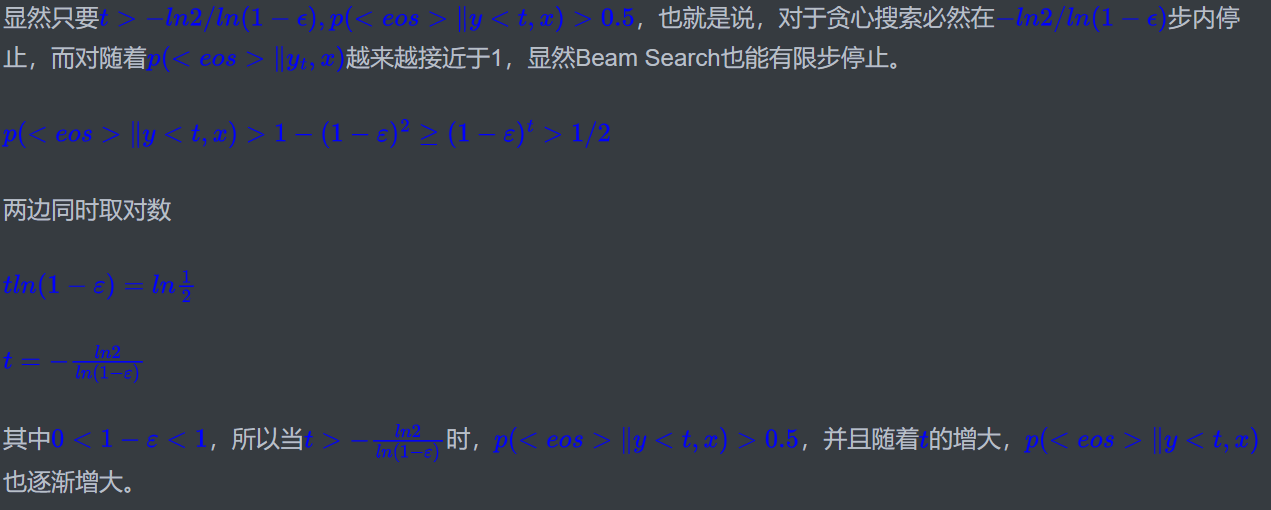
这两个结论只能用于随机解码，确定性解码就不能用了，因为没法保证一定能碰到，因此可以使用下面方法

3、自截断：这是论文稍微有意义的地方，自截断说白了就是随着解码过程，我们希望能碰到，这样就能停下来了，并且希望随着解码长度的增加碰到的概率也越来越多大，最终趋于1，这样就可以停下来了。定义

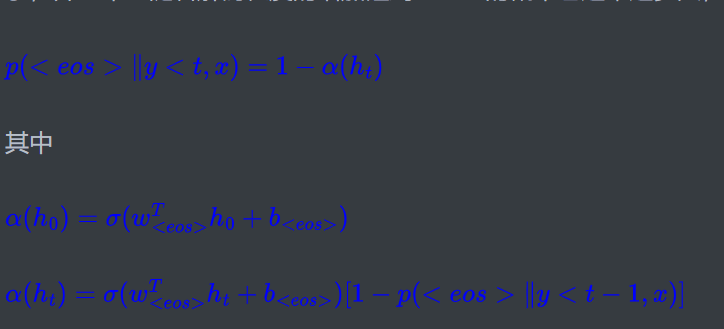
这里$\color{blue}{\sigma(·)}$将$\color{blue}R$映射到$\color{blue}{[0,1-ϵ]}$，例如可以用$\color{blue}{\sigma(·)=(1-ϵ)sigmoid(·)}$。设计好$\color{blue}{p(|y<t,x)}$，剩下的token概率按照原来的softmax方式计算，然后乘以$\color{blue}{ \alpha (h_t)}$即可。现在有

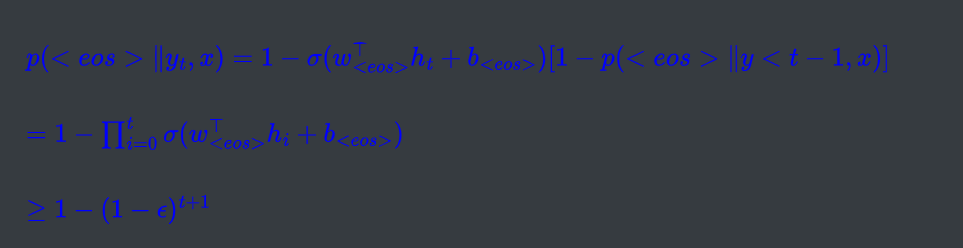
预测文本	hyp.text : 3 定期组织绩效考核指标目标完成情况进行过程管控
top 0 best_hyp.abstract	绩效考核指标考核指标
top 1 best_hyp.abstract	绩效考核指标考核指标目标
top 2 best_hyp.abstract	绩效考核指标考核指标目标指标

问题：重复

重复问题寻因探究

AAAI2021有一篇论文从理论上分析了seq2seq重复解码的现象，本质上，重复和不停是同理的，算是填补了上面论文的空白，论文链接A Theoretical Analysisi of the repetition Problem in Text Generation。

先量化以下问题，解码过程中子序列$\color{blue}{s=[w_1,w_2,…,w_n]}$后面接子序列$\color{blue}{t=[w_1,w_2,…,w_n,w_1]}$，我们就称$\color{blue}{w_1,w_2,…,w_n}$是一个$\color{red}{”重复子序列”}$，而我们要做的就是分析解码过程中重复子序列的概率。

二元解码

一般的自回归形式为: $\color{blue}{p(y|x)=\prod_{t=1}^lp(y_t|y_{y\lt t,x})}$，可以看出位置t 的解码不仅依赖输入x ，还依赖t 之前已经获得的所有解码结果，我们考虑简单的情况，做个马尔可夫假设，每一步解码只依赖前一时刻的结果，与再之前的无关，即$\color{blue}{\prod_{t=1^lp(y_t|y_{t-1},x)}}$，这样对于固定的x 而言，解码器实际上就是一个$\color{blue}{n\times n}$的转移矩阵$\color{blue}{P=(P_{i,j})}$，其中$\color{blue}{P_{i,j}}$表示从i 后面接j 的概率，n 代表词表大小，还需要一个结束标记，遇到就停止解码，所以实际上转移矩阵是$\color{blue}{(n+1)\times(n+1)}$，但是我们考虑的重复解码都是终止之前，所以只需要考虑$\color{blue}{n\times n}$就可以了。

我们要计算的是重复子序列出现的概率，假设$\color{blue}{[i,j,k]}$，是一个三元重复子序列，那么它出现概率就是序列$\color{blue}{[i,j,k,i,j,k,i]}$出现的概率：

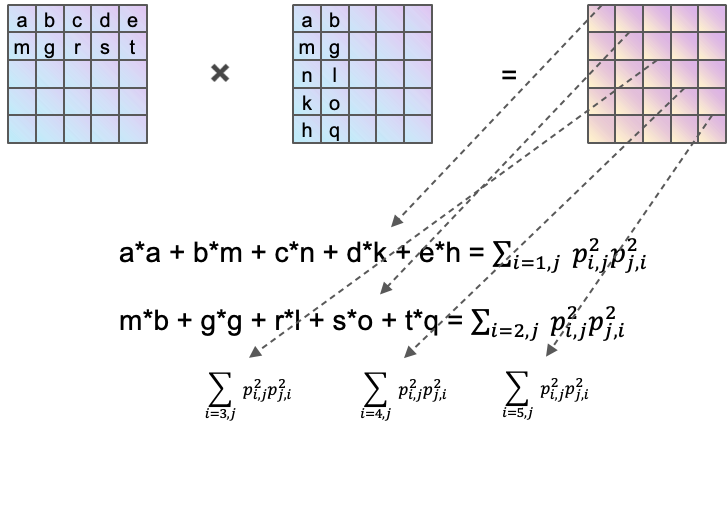
$\color{blue}{P_{i,j}P_{j,k}P_{k,i}P_{i,j}P_{j,k}P_{k,i}=P_{i,j}^2p_{j,k}^2P_{k,i}^2}$

因此所有的三元重复子序列的概率为：

$\color{blue}{\sum_{i,j,k}P_{i,j}^2P_{j,k}^2P_{k,i}^2=Tr(P\otimes P)^3}$

这里的$\color{blue}{\otimes}$表示逐位元素对应相乘，而$\color{blue}{Tr}$则是矩阵的迹，即对角线元素之和。最后我们将所有长度的重复子序列概率都加起来：

$\color{blue}{R=\sum_{k=1}^{\infty}}Tr(P\otimes P)^k=Tr(\sum_{k=1}^\infty(P\otimes P)^k)$

两个矩阵对应位置$\color{blue}{\otimes}$的目的就是为了使得每个位置上的值变为原来的平方，因此就实现了$\color{blue}{P_{i,j}P_{j,k}P_{k,i}P_{i,j}P_{j,k}P_{k,i}=P_{i,j}^2p_{j,k}^2P_{k,i}^2}$的目的。

$\color{blue}{(P\otimes P)^k}$中的k 实际上表示k 元重复子序列，那为什么这个k 次方的矩阵求迹就是结果了？以$\color{blue}{k=2}$为例（其中蓝色矩阵中的每一项都是平方项，只不过我并没有显式的标出平方）

对角线上每一个元素代表固定i 而遍历j 的结果，那么把所有的对角线都加起来（迹），实际上就是做了一个$\color{blue}{\sum_i}$的操作。

这就是二元解码出现重复解码的概率，目前只是一个理论公式，不过是我们重要的出发点，分别推到它的上下界。

一个下界

直接看$\color{blue}{R}$的公式看不出啥，我们可以给他先推到一个直观的下界，以三元重复子序列为例可以得到如下：

$\color{blue}{\sum_{i,j,k}P_{i,j}^2P_{j,k}^2P_{k,j}^2=n^3\times\frac{\sum_{i,j,k}P_{i,j}^2P_{j,k}^2P_{k,i}^2}{n^3}\gt n^3\times(\frac{\sum_{i,j,k}P_{i,j}^2P_{j,k}^2P_{k,i}^2}{n^3})^2=\frac{(TrP^3)^2}{n^3}}$

上面的推到可以通过均值不等式得到，$\color{blue}{\sqrt{\frac{\sum x^2}{m}}\ge \frac{\sum x}{m}}$两边同时平方就医得到$\color{blue}{\frac{\sum x^2}{m}\ge (\frac{\sum x}{m})^2}$。

$\color{blue}{\frac{(TrP^3)^2}{n^3}}$就是下界，但是我们可以做的更精细一点。假设P 矩阵中有一些元素为0，那么$\color{blue}{P_{i,j}^2P_{j,k}^2P_{k,j}^2}$中非零元素的个数就不是$\color{blue}{n^3}$，我们假设非零元素的个数为$\color{blue}{N_3(P)\lt n^3}$，那么我们在利用均值不等式的时候，可以只对非零元素进行，替换后如下：

$\color{blue}{\sum_{i,j,k}{P_{i,j}^2P_{j,k}^2P_{k,i}^2}\ge\frac{(TrP^3)^2}{N_3(P)}}$

其中$\color{blue}{N_3(P)}$的直接计算也比较困难，没有一般的通项公式，但我们可以做一个简单的估算：设$\color{blue}P$的非零元素的比例为$\color{blue}{\zeta}$，也就是非零元素的个数为$\color{blue}{\zeta n^2}$，那么我们一个认为$\color{blue}{P_{i,j}^2P_{j,k}^2P_{k,i}^2}$的非零元素比例近似为$\color{blue}{\zeta^3}$，而总的排列数为$\color{blue}{n^3}$，所以我们可以可以认为$\color{blue}{N_3(P)\backsim\zeta^3n^3}$。注意可以举例说明这个既不能保证上界，也不能保证下界，所以替换后无法保证等号成立。不过如果我们愿意相信是一个足够好的近似，那么可以写下

$\color{blue}{\sum_{i,j,k}{P_{i,j}^2P_{j,k}^2P_{k,i}^2}\ge\frac{(TrP^3)^2}{\zeta^3n^3}}$

以及

$\color{blue}{R=\sum_{k=1}^{\infty}Tr(P\otimes P)^k\ge\sum_{k=1}^{\infty}\frac{(TrP^k)^2}{\zeta^kn^k}}$

或者我们不关心等号，而将最右面的结果视为R 的一个估计。

初步结论

解码概率经过softmax出来，结果都不等于0，那么$\color{blue}{\zeta}$应该恒等于1，因此引入$\color{blue}{\zeta}$似乎没有什么价值。

事实上，softmax确实不会产生0概率值，但是解码算法通常会强制为零，在三种随机性解码以及两种确定性解码中，除了不靠谱的随机性解码中的原始采样随机解码外，其他都会或多或少确定若干个最优结果来作为候选值，这就相当于直接截断了转移概率矩阵，大大的降低了$\color{blue}{\zeta}$（非零概率）。

比如Greedy Search中，容易推出实际上对应这最小的非零概率$\color{blue}{\zeta=1/n}$，由于$\color{blue}{\zeta}$在公式的分母位置，因此$\color{blue}{\zeta}$的缩小就意味着重复了$\color{blue}{R}$的增加，这也就证明了Greedy Search的重复解码风险是相当高的，这也与实际中现象一致，也证明了在Beam Search中，我们Beam size取得越大，越不容易重复（仍会出现），但是会增加计算量。

一个上界

$\color{yellow}{下界能帮我们解释一些现象，而上界则可以给我们提供改进思路。}$

为了推导上界，我们利用如下的两个结论

1、矩阵的迹等于它所有特征值的和

2、如果$\color{blue}{\lambda_1(A)\ge\lambda_2(A)\ge…\ge\lambda_n(A)}$是矩阵$\color{blue}{A}$的所有特征值，那么$\color{blue}{\lambda_1^k(A)\ge\lambda_2^k(A)\ge…\ge\lambda_n^k(A)}$是矩阵$\color{blue}{A^k}$的所有特征值。

所以可以推导：

$\color{blue}{R=\sum_{k=1}^{\infty}Tr(P\otimes P)=\sum_{k=1}^{\infty}\sum_{i=1}^n\lambda_i((P\otimes P)^k)}$

$\color{blue}{=\sum_{k=1}^{\infty}\sum_{i=1}^{n}\lambda_i^k(P\otimes P)=\sum_{i=1}^{n}\sum_{k=1}^{\infty}\lambda_i^k(P\otimes P)}$

$\color{blue}{=\sum_{i=1}^n\frac{\lambda_i(P\otimes P)}{1-\lambda_i(P\otimes P)}}$

上述过程用到了级数$\color{blue}{\frac{x}{1-x}=\sum_{k=1}^{\infty}x^k}$，该级数只有在$\color{blue}{|x|\lt1}$才收敛，而很巧的是，我们可以证明$\color{blue}{P\otimes P}$的特征值绝对值必然不大于1，且通常都小于1：由于$\color{blue}{P}$是转移矩阵，因此它的每一行之和都为1，因此$\color{blue}{(P\otimes P)x=\lambda x}$，不失一般性，设$\color{blue}{x}$绝对值最大的元素为$\color{blue}{x_1,P\otimes P}$的第一个行向量为$\color{blue}{q_1^\top}$，那么我们有$\color{blue}|\lambda| |x_1|\le|q_1^{\top}x|\le|x_1|$，从而$\color{blue}{|\lambda|\le 1}$，并且等号成立的条件还是比较苛刻的，所以通常来说$\color{blue}{|\lambda|\lt 1}$。

注意函数$\color{blue}{\frac{x}{1-x}}$在区间[-1,1]区间是单调递增的，所以公式中主导的是第一项，如果非要给整体弄上一个上界，那么可以是$\color{blue}{\frac{n\lambda_i(P\otimes P)}{1-\lambda_i(P\otimes P)}}$。

再次结论

由此可见，如果想要降低重复率$\color{blue}{R}$，那么我们需要想办法降低矩阵$\color{blue}{P\otimes P}$的最大特征值。$\color{blue}{P\otimes P}$是一个非负矩阵，根据非负矩阵的$\color{yellow}Frobenius介值定理(非负矩阵的最大特征值在它每一行的和的最小值与最大值之间)$，我们有：

$\color{blue}{min_i\sum_{j}P_{i,j}^2\le\lambda_1(P\otimes P)\le max_i\sum_jP_{i,j}^2}$

现在我们知道，为了降低$\color{blue}{P\otimes P}$的最大特征值，我们需要想办法降低它的每一行之和，即$\color{blue}{\sum_jP_{i,j}^2}$，并且由于均值不等式

$\color{blue}{\sum_jP_{i,j}^2\ge n(\frac{\sum_jP_{i,j}}{n})^2=1/n}$

知它的最小值为$\color{blue}{1/n}$，在$\color{blue}{P_{i,1}=P_{i,2}=…=P_{i,n}}$时取到，因此最终我们得出结论：$\color{yellow}{要降低最大特征值，就要使得矩阵P每一行尽可能均匀，换言之，要降低P每一行的方差}$。

怎么降低方差呢，简单点来说就不能出现过高的概率值即可，比如某一行接近one hot的形式，那么平方之后仍然接近one hot的形式，那么求和就接近1，远远大于理论最小值$\color{blue}{1/n}$。实际中什么情况会出现过高的概率值呢，就是在某些字后面可以接的字很少，甚至只有一个候选项的时候，比如“忐”后面接“忑”，那么$\color{blue}{P_{i=忐}P_{j=忑}}$就相当高。那么怎么来避免出现这种过高的概率值呢，就是将高概率值得字合并起来，当作一个新词来看，那么“忐”哪一行就不存在，也就是无所谓得方差大了。

说白了，在文本生成任务中，以词为单位比以字为单位更加靠谱，更加不容易出现重复解码。适当地合并一些相关程度比较高的词作为新词加入到词表中，降低转移矩阵的方差，有助于降低重复解码的风险，原论文还给这个操作起了个很高端的名字，叫做Rebalanced Encoding Algorithm，事实上就是这个意思。

一般解码

那这个证明过程容易推广到一般的自回归模型中吗？很遗憾，并不容易。对于一般的自回归模型来说，它相当于每一步的$\color{blue}{P}$都是不一样的，因此只要模型的性能足够好，其实基本上不会出现重复解码，事实上经过充分预训练的生成式模型，确实很少出现重复解码了。但是，我们又能观察到，哪怕是一般的自回归解码，偶尔也能观察到重复解码现象，尤其是没有经过预训练的模型，这又该怎么解释呢？

前面的小节是基于二元解码模型的，结论是二元解码模型确实容易出现重复解码，那么我们或许可以反过来想，一般的自回归模型出现重复解码现象，是因为它此时退化为了二元解码模型？对于难度比较高的输入，模型可能无法精细捕捉好每一步的转移概率，从而只能将转移矩阵退化为二元解码，这是有可能的。

预测文本	hyp.text : 负责人员招募工作确保公司业务可持续性发展
top 0 best_hyp.abstract	业务发展策略
top 1 best_hyp.abstract	业务发展策略公司
top 2 best_hyp.abstract	业务发展策略公司发展

问题：生成原文没有的词（统称为产生新词），这并不是想要的

引入先验知识，我们生成得词都是句子中出现得（出现并不一定连续）。这样以来，我们可以利用句子（文章）中得词集作为一个先验分布，加到解码过程得分类模型中，使得模型在解码输出时更倾向选用文章中已有得字词。

具体来说，就是在每一步预测时，我们得到总向量$\color{blue}{x}$（它应该是decoder当前的隐层向量、encoder的编码向量、当前decoder与encoder的Attention编码三者的拼接），然后得到全连接层，最终得到一个大小为$\color{blue}{|V|}$得向量$\color{blue}{y=(y_1,y_2,…,y_{|V|})}$，其中$\color{blue}{|V|}$就是词表得词数。经过softmax后得到原本得概率$\color{blue}{p_i=\frac{e^{y_i}}{\sum_ie^{y_i}}}$，这就是原始得分类方案。引入先验分布得方案是，对于每个句子（文章）我们得到一个大小为$\color{blue}{|V|}$得0/1向量$\color{blue}{x=(x_1,x_2,…,x_{|V|})}$，其中$\color{blue}{x_i=1}$意味该词在文章中出现过，负则为0。将这样一个0/1向量经过缩放平移层得到：

$\color{blue}{\hat y=s\otimes x+t=(s_1x_1+t_1,s_2x_2+t_2,…,s_{|V|}x_{|V|}+t+{|V|})}$

其中$\color{blue}{s,t}$为训练参数，然后将这个向量与原来得$\color{blue}{y}$取平均后才做softmax：

$\color{blue}{y = \frac{y+\hat y}{2},p_i=\frac{e^{y_i}}{\sum_ie^{y_i}} }$

经实验，这样先验分布得引入，有助于加快收敛，生成更好得短句（标题）