Abstract

在摘要中作者提到，通过学习一个分布式的词表示来克服维数的诅咒，它允许每个训练句子向模型告知一个指数数量的语义相邻句子。该模型同时学习 (1) 每个单词的分布式表示，以及 (2) 用这些表示 表示的单词序列的概率函数。

Introduction

在介绍中，作者举例到，如果相对10000个词建立连续10个词得联合分布，那么可能需要得参数是$10000^{10}-1$，当对连续变量进行建模时，我们比较容易获得泛化（光滑得函数类，神经网路模型，高斯模型等），对于离散空间泛化结构就不明显了，每个离散变量得取值很大时，大多观测对象在汉明距离上几乎是最大得。

本文提出在高维情况下，重要的是将概率质量均匀分布在每个训练点周围的各个方向上。这里提出得泛化方式也与之前最先进得统计方法模型不同。

语言得统计模型公式如下$P({w_1}^T)=\prod_{t=1}^T(P(w_t|w_1^{t-1}))$我们可以看出，每次计算t得概率时，都需要从1~t-1的概率，这无形中就增加了很大的计算量，本文利用统计上词序更加依赖暂时距离较近的词这一事实，因此提出了n-gram模型结构，计算公式如下$P(w_t|w_1^{t-1})=P(w_t|w_{t-n+1}^{t-1})$。

在文本中总会出现上下文连续的词但预料中没有出现的情况，一种简单的解决办法就是将n回退到三元模型。从本质上说一个新的单词序列是通过“粘合”非常短的长度为1,2…或者在训练数据中经常出现的单词上。获取下一个片段概率的规则隐含在后退或插值n-gram算法的细节中。研究中一般采用3，但显然，单词前面的序列中又更多的信息需要预测，并不仅仅时单词前的两个单词。因此该方法至少需要两点需要改进

• 它不考虑超过1到2个单词的上下文
• 不考虑单词之间的“相似性”

Fighting the Curse of Dimensionality with Distributed Representations

论文提出方法思想总结如下：

1. 将vocabulary的每个单词关联到一个分布式单词特征上（$R^m$）

2. 将词序列中的词的特征向量表示为词序列的联合概率函数

3. 同时学习单词特征向量和联合概率函数的参数

特征向量的不同维度表示单词的不同方位，每个单词的都与向量空间中的一个点相关联，特征的维度m远小于词汇表大小，概率函数表述为给定前一个词的情况下下个词的条件概率的乘积

A Neural Model

论文提出的模型结构如下图所示：

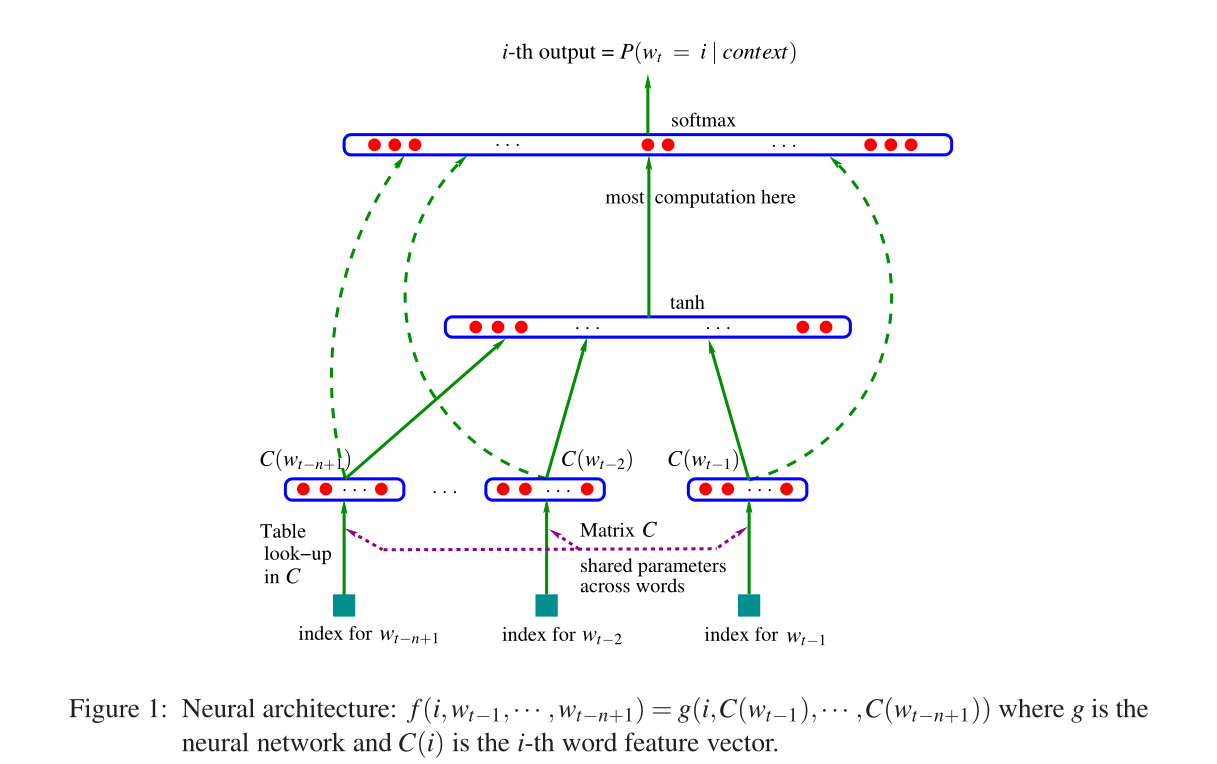
Neural architecture

上图输入是$W_{t-n+1}、…、w_{t-2}、w_t$，本质上就是通过前面n-1个词预测第t个词，这也就是n-gram模型

• $C(w_{t-n+1})$：t-n+1单词对应的词向量，也是模型最终的收获；
• C：矩阵，行是vocab，列是word对应的词向量$|V*m|$；

模型的输入即把单词concat通过隐藏层，最后通过tanh激活，模型最后输出层公是如下：$y=b+Wx+Utanh(d+Hx)$，最后加的这一项是中间隐藏层的表示，其中x的表示如下：$x=(C(w_{t-1}),C(w_{t-2}),…,C(w_{t-n+1}))$。

【论文第三部分提出两种训练加速方式，一种是内存共享，另一种是参数共享】