早上看到了Glove,细思之下发现了解不多,于是抽空网上搬砖。
Glove是何方妖孽
Glove 全称 Global Vectors for Word Representation,基于全局词频统计的词表征,是一种词嵌入方式,将高维稀疏向量表示为低维稠密向量,并且保留了词与词之间的相似性(即cos距离更近)。
Glove来龙去脉
三步曲实现Glove
- 一步预备
根据corpus构建一个共现矩阵(Co-ocurrence Matrix)$\color{blue}{X}$,什么是共现矩阵呢?先补充一个基本概念;
共现:给定一个语料库,一对单词的再上下文窗口同时出现的次数
上下文窗口:给定一个单词的上下文几个单词以内范围的大小,例如指定2,$\color{blue}{w_1,w_2,w_3,w_4,w_5,…}$,$\color{blue}{w_3}$的上下文就包含了$\color{blue}{w_1到w_5}$
假设我们有一个corpus如下:
我爱中国; 我爱北京; 我爱天安门; 我爱我家;假设content window size = 2,就可以得到如下的矩阵
我 爱 中 国 北 京 天 安 门 家 我 0 4 1 1 1 1 1 1 1 1 爱 0 1 1 1 1 1 1 1 1 中 0 1 0 0 0 0 0 0 国 0 0 0 0 0 0 0 北 0 1 0 0 0 0 京 0 0 0 0 0 天 0 1 1 0 安 0 1 0 门 0 0 家 0 共现矩阵是一个对阵矩阵,因此下三角省了。
矩阵中每一个元素$\color{blue}{X_{ij}}$代表单词$i$和单词$j$再content window size内共现的次数,一般而言,content window size最小位1,而Glove中根据两个单词再窗口的距离$d$提出了一个衰减函数$\color{blue}{decay = 1/d}$来计算权重,距离越远的单词再总计数的权重越小,这也符合常理,越“远”越“远”。
- 二步走
根据共现关系构建词向量,两者关系如下:
$\color{blue}{ {w_i^T} \hat{w_j} + b_i+\hat{b_j}=log(X_{ij})—–(1)}$
其中:$\color{blue}{w_i和\hat{w_j}}$是最终的词向量,$\color{blue}{b_i和b_j}$分别是两个词向量的偏置。
- 三步停
根据公式(1)构造损失函数如下:
$\color{blue}{J=\sum_{i,j}^Vf(X_{ij})(W_i^T\hat{w_j}+b_i+\hat{b_j}-log(X_{i,j}))^2—–(2)}$
可以看出是一个均方误差函数(mean square loss),额外加了个权重函数$\color{blue}{f}$,这个权重函数如下:
$f(x)$的原因如下:
- 经常一起出现的单词对权重要大于很少出现的单词对,所以是个非递减函数
- 随着单词对一起出现的次数越多,希望权重不要一直增大
- 未出现的单词对,不要参与loss的计算,即为0
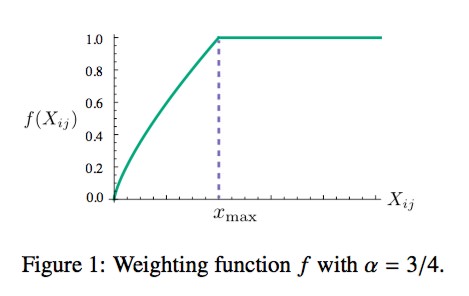
论文中$\color{blue}\alpha$取值为0.75,$\color{blue}{x_{max}}$取值100。
Glove的运动方式
Glove是一种无监督的学习方式,但是其实是有label的,这一点和word2vec一样;而Glove的label就是公式(2)中的$\color{blue}{log(X_{ij})}$,两个$w$就是需要学习更新的参数,所以本质上和监督学习的方式没什么不同,都是基于梯度下降。
论文中采用AdaGrad梯度下降法,对矩阵$X$中所有非0元素进行随机采样,学习率0.05,再vector size 300的情况下迭代50次,再其他vector size上迭代100次,直至收敛;最后得到两个vector, 分别是$\color{blue}{w}$,$\color{blue}{\hat{w}}$,因为$X$是对称的,因此理论上,$\color{blue}{w}$,$\color{blue}{\hat{w}}$也是对称的,他们唯一的区别是初始化时参数不同,导致最后的结果有差异,为了更好的鲁棒性,我们最终将两者之和作为最终的vector
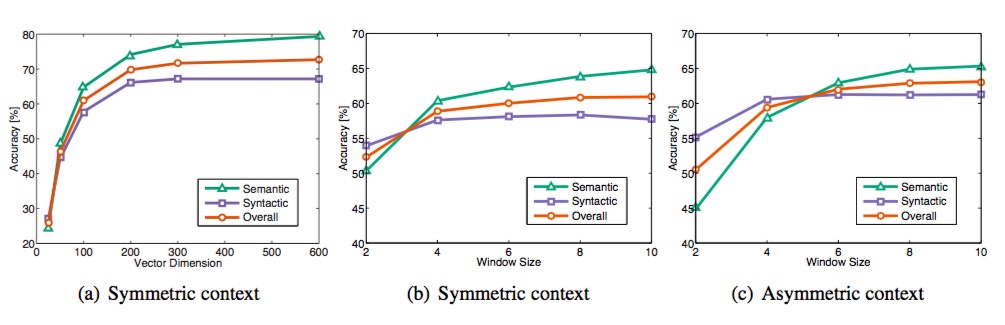
这个图一共采用了三个指标:语义准确度,语法准确度以及总体准确度。那么我们不难发现Vector Dimension在300时能达到最佳,而context Windows size大致在6到10之间。
Glove 公式(1)探因
公式(1)不得不写下来呀,抄也得抄下来,遵循书读百遍,其意自现,下面就开始愉快的抄写吧!
定义一些变量:
$\color{blue}{X_{ij}}$:单词$j$出现再单词$i$的上下文的次数
$\color{blue}{X_i}$:单词$i$的上下文中出现所有单词出现的总次数,即$\color{blue}{X_i=\sum^kX_{ik}}$
$\color{blue}{P_{ij}}$:$\color{blue}{P(j|i)=\frac{X_{ij}}{X_i}}$,表示单词$j$出现在单词$i$的上下文中的概率
| Probability and Ratio | k=solid | k=gas | k=water | k=fashion |
|---|---|---|---|---|
| $P(k|ice)$ | $\color{blue}{1.9*10^{-4}}$ | $6.6*10^{-5}$ | $3.0*10^{-3}$ | $1.7*10^{-5}$ |
| $P(k|steam)$ | $\color{blue}{2.2*10^{-5}}$ | $7.8*10^{-4}$ | $2.2*10^{-3}$ | $1.8*10^{-5}$ |
| $P(k|ice)/P(k|stream)$ | $\color{blue}{8.9}$ | $8.5*10^{-2}$ | $1.36$ | $0.96$ |
通过上面的表格可以分析得出,当k=solid时,$\color{blue}{P(solid|ice)/P(solid|stream)}$比1大很多,这说明solid和ice相比solid和steam更相关,其他同理。由此得出结论,通过概率比率相比概率本身学习词向量可能是一个更恰当的方法。
为了达到上述目标,构造函数
$\color{blue}{F(w_i,w_j,\hat{w_k})=\frac{P_{ik}}{P_{jk}}—–(4)}$
利用向量空间的线性结构做差,可以得到
$\color{blue}{F(w_i-w_j,\hat{w_k})=\frac{P_{ik}}{P_{jk}}—–(5)}$
我们可以发现公式(5)右边是一个常数,左边为了表达两个概率的比例差,左边变成两个向量的内积,如下
$\color{blue}{F((w_i-w_j)^T,\hat{w_k})=\frac{P_{ik}}{P_{jk}}—–(6)}$
接下来就到高能时刻了,先补充一波电,同态特性,首先$X$是对称矩阵,单词和上下文单词是相对的,因此我们可以做如下交换$\color{blue}{w<->\hat{w_k},X<->X^T}$,公式(6)应该保持不变,为了满足这个条件,要求函数$F$满足同态特性:
$\color{blue}{F((w_i-w_j)^T,\hat{w_k})=\frac{F(w_i^T\hat{w_k})}{F(w_j^T\hat{w_k})}—–(7)}$
结合公式(6),得到
$\color{blue}{F(w_i^T)=P_{ik}=\frac {X_{ik}} {X_i} —–(8)}$
令F=exp,可以得到下面公式(9)
$\color{blue}{w_i^T\hat{w_k}=log(P_{ik})=log(X_{ik})-log(X_i)—–(9)}$
===>
$\color{blue}{log(X_{ik})=w_i^T\hat{w_k}+log(X_i)—–(10)}$
这里就和(1)很像了,我们把$log(X_i)$纳入到$w_i$的偏置中,为了对称性,也加到$\hat{w_k}$中,得到如下公式
$\color{blue}{log(X_{ik})=w_i^T\hat{w_k}+b_i+\hat{b_k}—–(11)}$